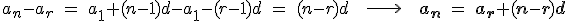En casa de mi tío hay varias estanterías de libros que están repletas. Los estantes de esas estanterías, están separados de forma periódica. La inferior está a 7 centímetros del suelo y las restantes a 34 centímetros cada una de la anterior. Si escribimos la altura a la que están los estantes, obtenemos la siguiente sucesión 7, 41, 75, 109, 143, 177, 211.
Las sucesiones que, como la anterior, tienen la característica de que cada término se obtiene del anterior sumándole una cantidad constante reciben el nombre de progresiones aritméticas.
Al valor constante que se suma a cada término para obtener el siguiente se le llama diferencia y suele representarse por la letra d. En el caso del ejemplo de la estantería la diferencia sería 34.
En general, en una progresión aritmética se cumple que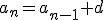 
para cualquier n a partir de 2.
Es muy fácil ver si una sucesión es una progresión aritmética. Basta restar pares de términos consecutivos; si se obtiene siempre el mismo valor, tenemos una progresión aritmética.
Por ejemplo, la sucesión 6, 10, 14, 18, 22, ... es progresión aritmética ya que se cumple:
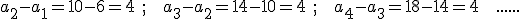
Una forma simple de verlo es hallar la diferencia entre los dos primeros términos y comprobar si sumando siempre ese valor se obtienen los demás.
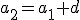
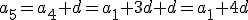
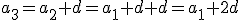
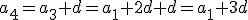
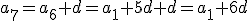
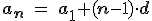
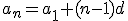y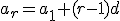 
, si restamos ambos podemos encontrar la fórmula para hallar un término en función de otro cualquiera.
