La ley de sucesión

Paul Foot. Mens 100m finals British Champs and Olympic Trials (CC BY-SA)

En la imagen adjunta puedes ver la parrilla de salida de una carrera de 100 metros lisos. En los Campeonatos Mundiales de Atletismo de Berlín en 2009 el jamaicano Usain Bolt superó el récord del mundo establecido hasta el momento, consiguiendo la marca de 9,59 segundos.

Si observas la tabla, verás que lo primero que hay asignado a cada calle es el número del dorsal del atleta que correrá por ella. Si consideramos esos números, nos encontramos con una serie de 8 números ordenados.

Con este tipo de conjuntos numéricos es con el que vamos a trabajar en esta unidad.

Importante

Llamaremos sucesión numérica a todo conjunto ordenado de números.

A cada uno de sus elementos se le llama término y se caracteriza por un subíndice que indica el lugar que ocupa en la sucesión. De esa forma a₃ representa el tercer término y el término decimocuarto se indicará por a₁₄.

Por ejemplo, la sucesión 1, 5, 14, 30, 55, 91, 144,... que encontraste en los pasatiempos del apartado 1, tiene como tercer término a₃= 14 y 144 es el término 7º.

Al término que ocupe un lugar cualquiera lo llamaremos término enésimo y lo representamos por a_n.

Hay veces en que los números que se han ordenado no tienen ninguna relación con el lugar que ocupan, como pasa con los dorsales de los atletas en la carrera, pero en otras ocasiones sí la tienen. En este caso existe una ley de formación, es decir, una fórmula que nos permite conocer cuál es el número que sigue a los que conocemos o que ocupa un lugar determinado. Gracias a esta fórmula, podemos conocer cuál es el término que ocupa un lugar cualquiera n, y lo llamaremos término general de la sucesión.

Por ejemplo, en la sucesión 2, 5, 8, 11, 14, .... puedes observar una clara regla de formación: cada número se obtiene sumando 3 unidades al número anterior, es por lo tanto, muy fácil hallar el número que continúa que será el 17. El término general de la sucesión sería a_n = 3n-1. Puedes comprobar fácilmente que si sustituyes n por 1, 2, 3, ... vas obteniendo los términos de la sucesión.

A veces, te encontrarás sucesiones en las que no exista un término general o una ley de formación, pero en las que, sin embargo, haya una propiedad que cumplan los números y que nos permita construir la sucesión. Por ejemplo, la sucesión 2, 3, 5, 7, 11, 13, 17, ... es la formada por los números primos y la 3; 3,1; 3,14; 3,141; 3,1415; ... está formada por las aproximaciones del número .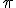

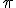Comprueba lo aprendido

Escribe el número que seguiría en cada serie de las siguientes.

1)	1, 2, 3, 4, 5, ...	3)	1, 4, 9, 16, 25, ...	5)	3, 6, 12, 24, 48, ...
2)	-5, 5, -5, 5, -5, ...	4)	25, 22, 19, 16, 13, ...	6)	0, 2, 6, 12, 20, ...

Pista: Para la última sucesión compárala con los terminos de la primera y la tercera.

Aprende a hacerlo

Vamos a hallar los términos generales de las sucesiones vistas en el ejercicio anterior.

Retroalimentación

1) En este caso, es muy fácil pues el valor coincide con la posición del término, por lo que el término general es .

2) Aquí tenemos el número 5 al que le cambia el signo. Es negativo en los lugares impares y positivo en los pares. Por lo tanto, basta multiplicar por una potencia de -1 conveniente. El término general sería . De esa forma, los lugares impares tendrían un signo menos y los lugares pares un signo más.

3) Aquí tenemos la sucesión de los cuadrados de los números naturales. Su término general es .

4) En cada término se resta 3 del anterior. Como para llegar al término n hemos restado 3 n-1 veces el término general sería o si operamos el paréntesis . Puedes comprobar que es el término general dando valores a n y viendo que obtienes los primeros términos de la sucesión.

5) Aquí estamos multiplicando por 2, igual que pasaba en el apartado anterior, para llegar al término n hemos tenido que multiplicar el primer término, 3, por el valor 2 un total de n-1 veces. Por tanto, el término general sería . Estos dos últimos tipos de sucesiones se estudiaran más detenidamente en los siguientes apartados.

6) La última es la más complicada, pues no es posible extraer la regla de formación a partir de los valores.a simple vista. Pero si nos fijamos en las anteriores sucesiones; podemos comprobar que, si le restamos miembro a miembro los términos de la tercera sucesión menos los de la primera, nos dan esos términos. Por tanto, su término general será

En el enlace tienes un ejemplo de patrón de construcción de figuras. Si aumentas n aparecen los siguientes términos del patrón. Al contar el número de cuadrados de cada figura y el de líneas que la forman obtenemos dos sucesiones. Tienes tres métodos diferentes para contarlos.

Consolación Ruiz Gil. Término General (forma T)

Dibuja en tu cuaderno el patrón y escribe una tabla que te indique el número de cuadrados y líneas que tiene cada término de la sucesión. Después, intenta encontrar el término general y escribe los cálculos que necesites para encontrarlo. Escribe la expresión final simplificada. Por último, pulsa en el botón de solución y comprueba si coincide con lo que has obtenido.

En la red

En el siguiente enlace accedes a una actividad del Proyecto Gauss. En ella se quiere diseñar un paseo formado por jardineras y losetas que las rodean.

Hay tres diseños posibles. Debes seleccionar uno de los tres y argumentar por qué has elegido ese diseño en lugar de los otros dos. Una vez que hayas elegido uno debes resolver las cinco primeras cuestiones que aparecen detrás de la ventana interactiva, pero no con el Diseño 1, si no con el que hayas elegido. Realiza la actividad en tu cuaderno.

En la red

Para practicar los conomientos adquiridos entra en el siguiente enlace y resuelve los dos primeros ejercicios que aparecen. Copia en tu cuaderno las soluciones que has encontrado.

Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0

Término siguiente
Serie 1	Serie 2	Serie 3	Serie 4	Serie 5	Serie 6
Rellenar huecos (1): JXUwMDZl	Rellenar huecos (2): JXUwMDZk	Rellenar huecos (3): JXUwMDZiJXUwMDA1	Rellenar huecos (4): JXUwMDY5JXUwMDAx	Rellenar huecos (5): JXUwMDYxJXUwMDBm	Rellenar huecos (6): JXUwMDZiJXUwMDAz