De las constantes numéricas que manejamos a diario en multitud de aspectos de nuestra vida, hay muy pocas que se mantengan constantes a lo largo de su evolución. Por ejemplo, es verdad que el número de portal de nuestra casa, nuestro DNI, nuestro número de móvil, el número de amigos cercanos, etc, puede que no cambien (al menos el DNI nunca); pero hay otros aspectos que si cambian con facilidad: nuestro peso, la estatura, el saldo de nuestros ahorros, etc.
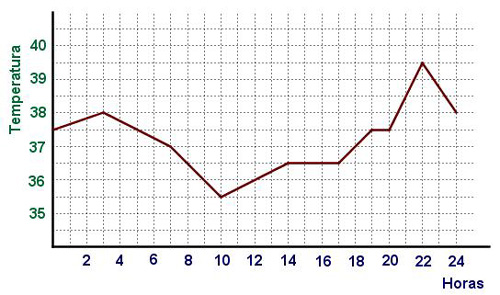
Si pensamos en un enfermo que se encuentra hospitalizado y al que regularmente se le toma la temperatura, está claro que lo normal es que la temperatura suba y baje a lo largo del día.
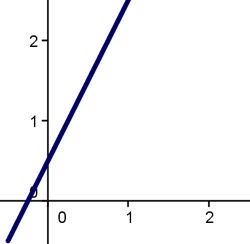
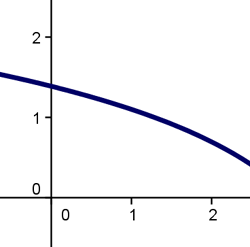
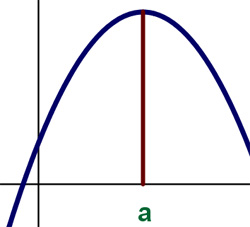
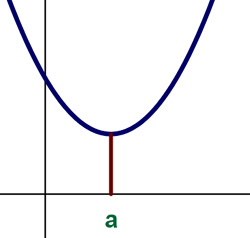
Vamos por tanto a tratar en este apartado los aspectos de crecimiento y de decrecimiento de una función.