 En una función se relacionan siempre dos números. El primero recibe el nombre de variable independiente, ya que puede tomar cualquier valor, y suele representarse por la letra x. Al segundo valor, que depende del valor que tuviese el nombre, se le llama variable dependiente y se le suele representar por la letra y.
En una función se relacionan siempre dos números. El primero recibe el nombre de variable independiente, ya que puede tomar cualquier valor, y suele representarse por la letra x. Al segundo valor, que depende del valor que tuviese el nombre, se le llama variable dependiente y se le suele representar por la letra y.
Por ejemplo, la recaudación de un cine, una determinada tarde, depende del número de espectadores que hayan entrado al cine. El número de espectadores sería la variable independiente y la cantidad recaudada la dependiente.
Las funciones suelen representarse por una letra minúscula siendo las más utilizas la f y siguientes. Para representar que un valor y depende de x se escribe 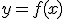 lo que se lee y es función de x. Es corriente también decir que y es la imagen de x mediante la función f, y que x es la antiimagen o antecedente de y.
lo que se lee y es función de x. Es corriente también decir que y es la imagen de x mediante la función f, y que x es la antiimagen o antecedente de y.
Por costumbre, a la variable independiente se le llama solo variable y a la variable dependiente se le llama función.
 En una función se relacionan siempre dos números. El primero recibe el nombre de variable independiente, ya que puede tomar cualquier valor, y suele representarse por la letra x. Al segundo valor, que depende del valor que tuviese el nombre, se le llama variable dependiente y se le suele representar por la letra y.
En una función se relacionan siempre dos números. El primero recibe el nombre de variable independiente, ya que puede tomar cualquier valor, y suele representarse por la letra x. Al segundo valor, que depende del valor que tuviese el nombre, se le llama variable dependiente y se le suele representar por la letra y.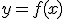 lo que se lee y es función de x. Es corriente también decir que y es la imagen de x mediante la función f, y que x es la antiimagen o antecedente de y.
lo que se lee y es función de x. Es corriente también decir que y es la imagen de x mediante la función f, y que x es la antiimagen o antecedente de y.