¡Toma corte!

Observa la gráfica que tienes al lado. En ella está representada la situación financiera de una empresa en los primeros años de vida.

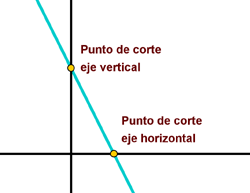
Lo que nos interesa que observes es la evolución de la gráfica y, sobre todo, el significado que tienen los puntos que están situados sobre los ejes de coordenadas. En primer lugar, parte del punto situado sobre el eje vertical en la que la variable tiempo (x) vale cero. Es lógico ya que se empieza a contar desde el momento en que se crea la empresa.

Al principio, el estado financiero es negativo; por los gastos necesarios para montar la empresa. Poco a poco, va aumentando y llega un momento en el que el estado financiero deja de ser negativo y se hace cero (y); que es cuando se ha recuperado el dinero invertido y, a partir de ahí, se comienza a ganar dinero.

Como has visto, los lugares en los que la variable o la función se hacen cero son importantes para saber la evolución de la relación presentada por la función.

Importante

El punto de corte de la función con el eje vertical, el de ordenadas, es aquel en el que la variable se hace cero. Por lo tanto, basta anular la variable en la función para obtener la ordenada del punto de corte. Es decir, en la función y=f(x) será un punto de la forma (0,f(0)).

Por su parte, el corte de la gráfica de la función con el eje de abscisas, el horizontal, corresponderá a un valor de x que anule la función. Es decir, si se verifica que f(a) = 0, entonces el punto de corte con el eje horizontal será (a,0).